The Sir Model For Spread Of Disease
The sir model for spread of disease. The SIR Model for Spread of Disease - The Contact Number. The SIR Model for Spread of Disease - Eulers Method for Systems. The SIR Model for Spread of Disease.
The SIR Model for Spread of Disease - Relating Model Parameters to Data. Compare your calculated value with the one you get by direct calculation from the definition c bk. The independent variable is time t measured in days.
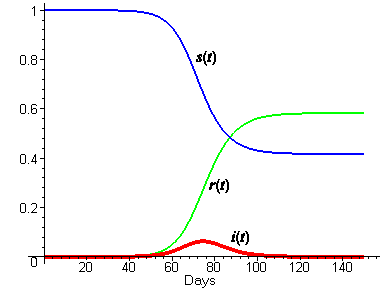
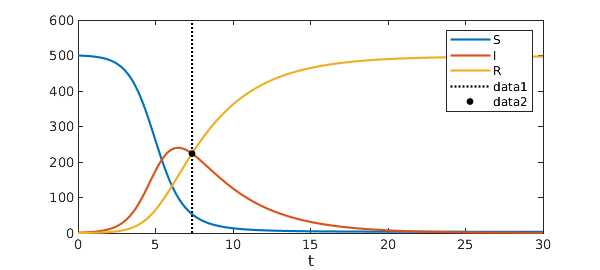
3 linhas The first set of dependent variables counts people in each of the groups each as a function of. The SIR Model for Spread of Disease - Relating Model Parameters to Data. During the winter of 1968-1969 the United States was swept by a virulent new strain of influenza named Hong Kong flu for its place of discovery.
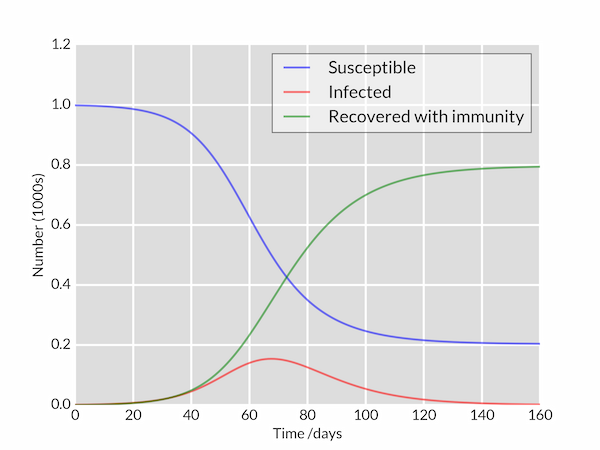
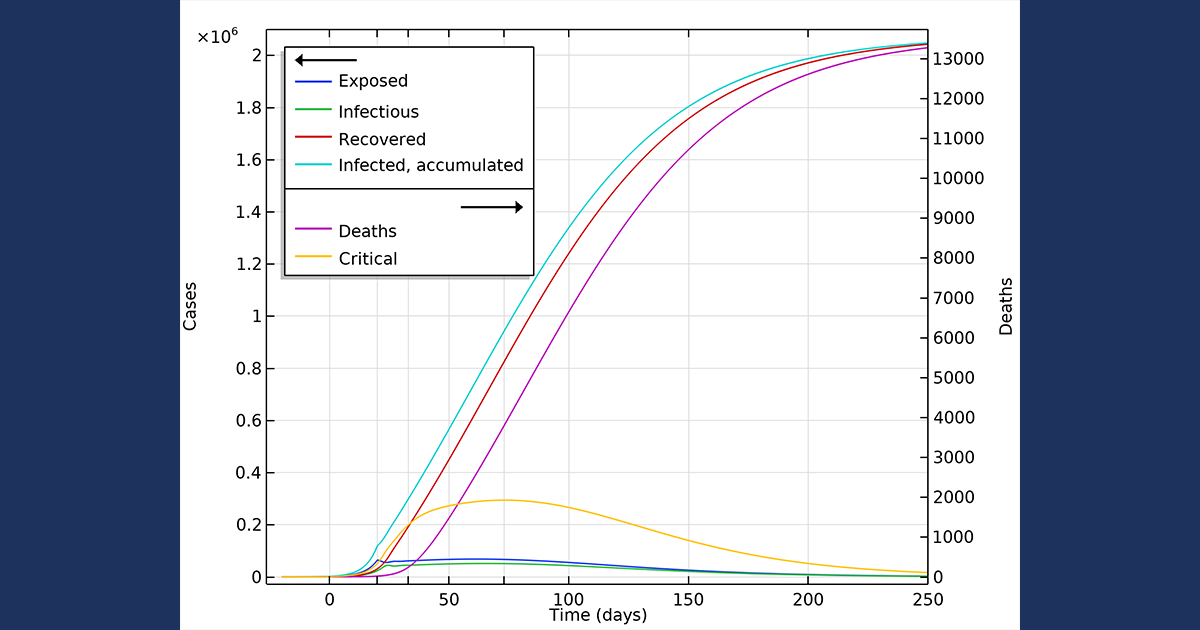
SIR model for COVID-19 According to this model and without any intervention to contain the spread the virus would be extinguished in about 180 days saving less than 20 of the population. The SIR Model for Spread of Disease. This is calculus as tool.
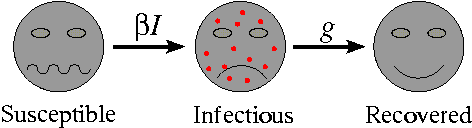
It examines how an infected population spreads a disease to a susceptible population which transforms into a recovered population. The use of mathematics to model the spread of infectious disease is an increasingly critical tool not just for epidemiologists and health care providers. Initial exploration of model.
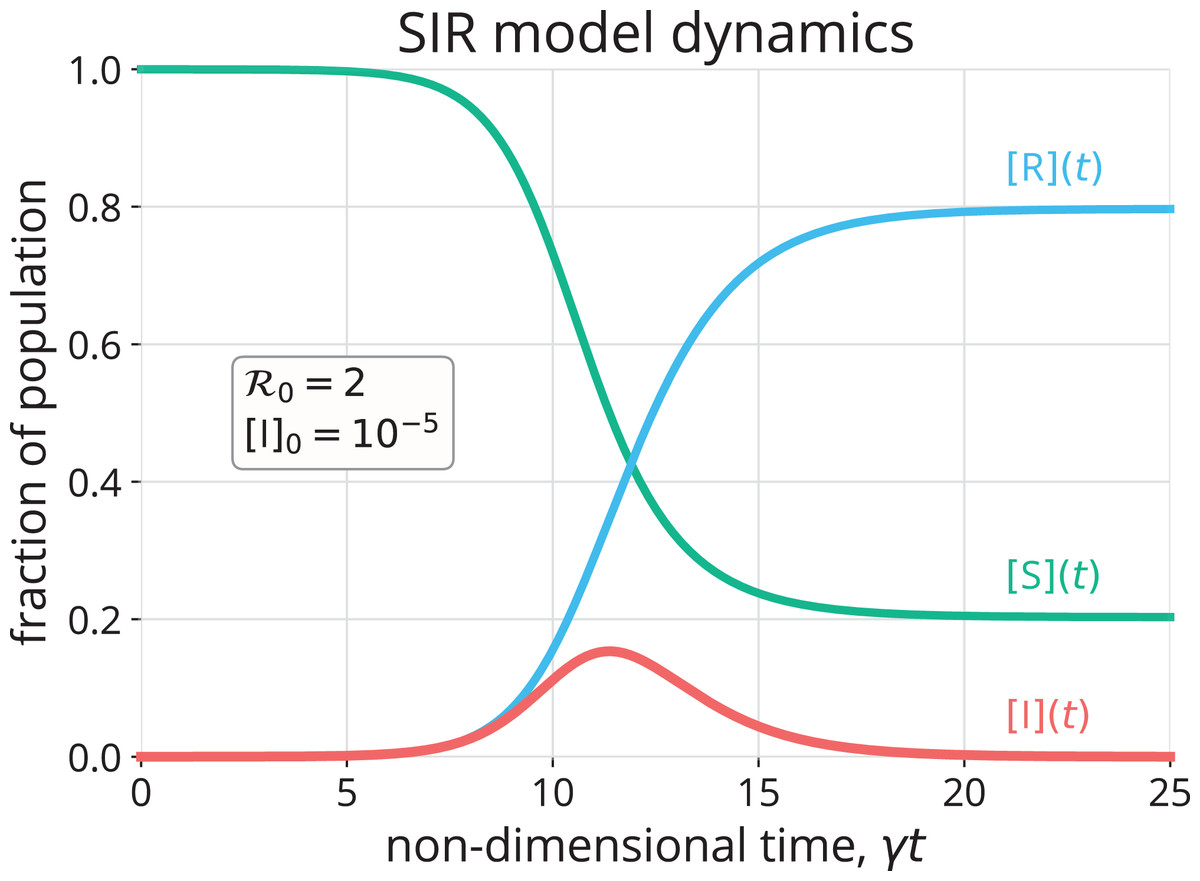
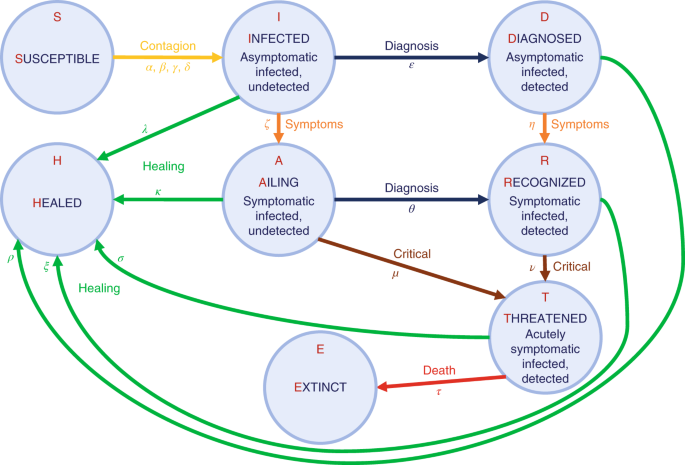
SIR model is of course a very simple model not suitable for shaping complex dynamics especially those which involve large and different populations. David Smith and Lang Moore The SIR Model for Spread of Disease - The Contact Number Convergence December 2004 JOMA. The SIR Model for Spread of Disease - Background.
The SIR Model for Spread of Disease. The SIR Model for Spread of Disease - Herd Immunity.
Compare your calculated value with the one you get by direct calculation from the definition c bk.
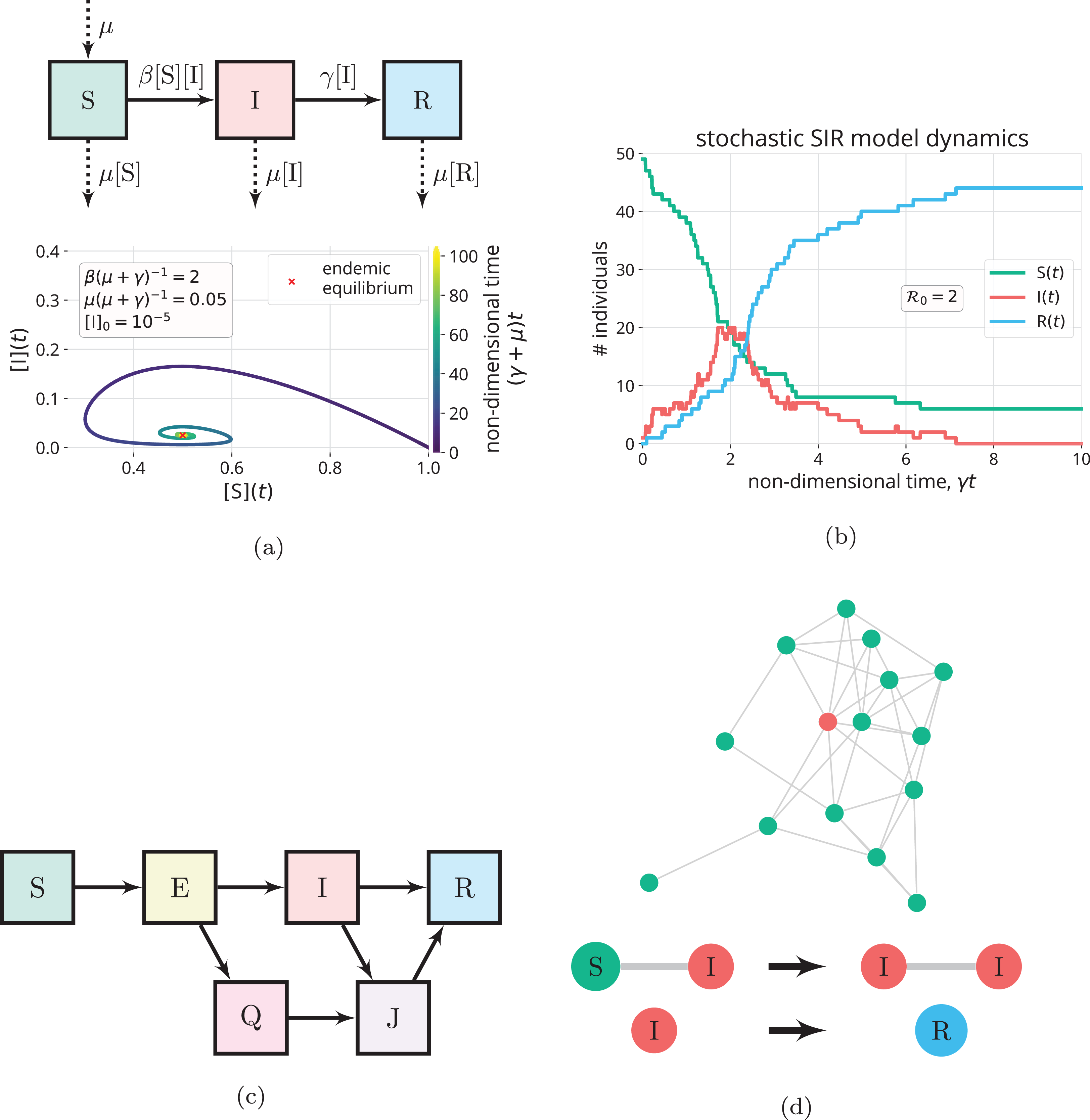
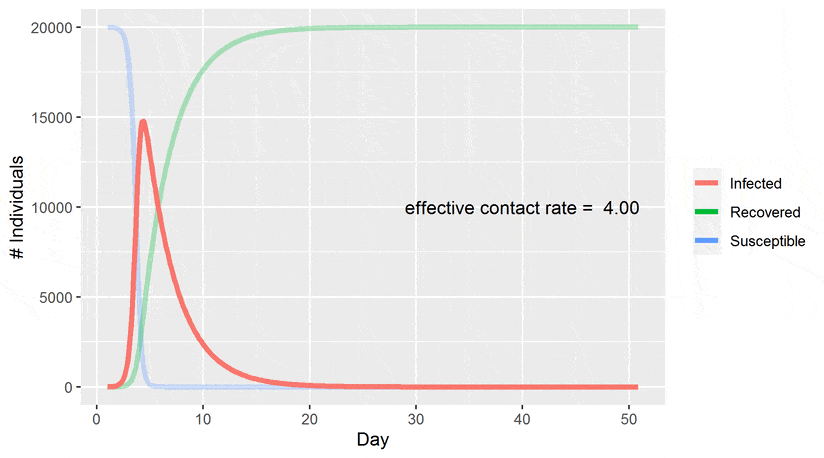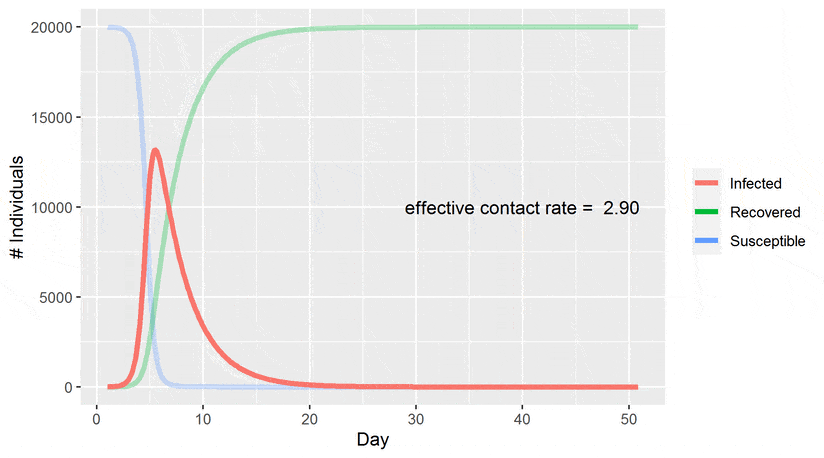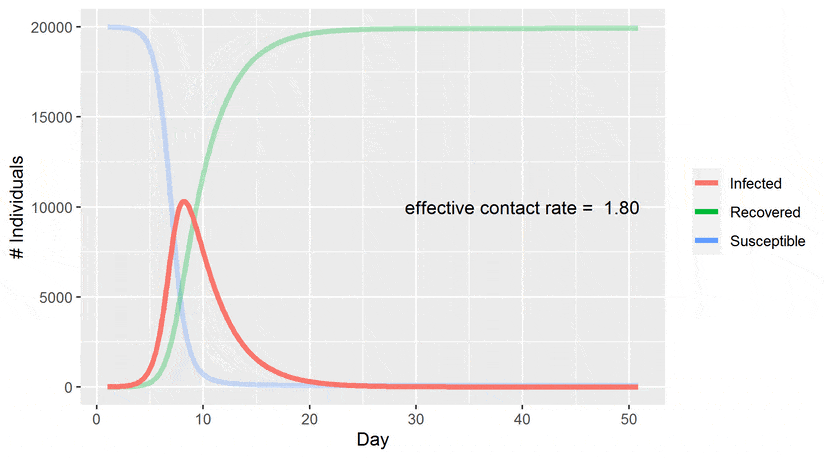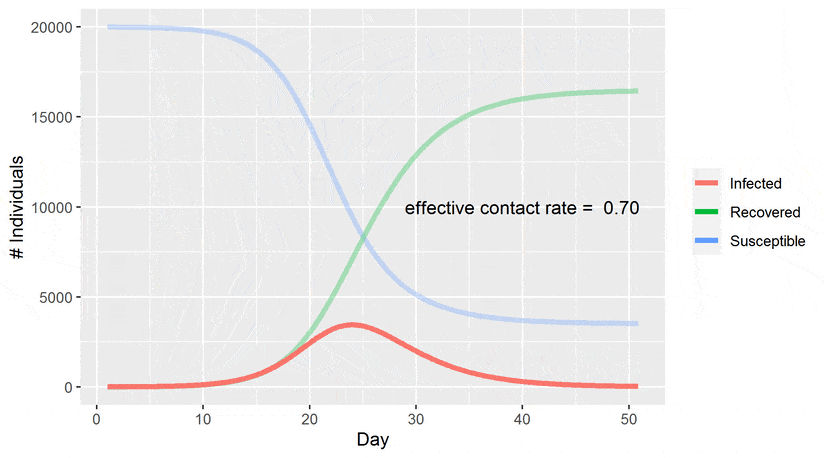
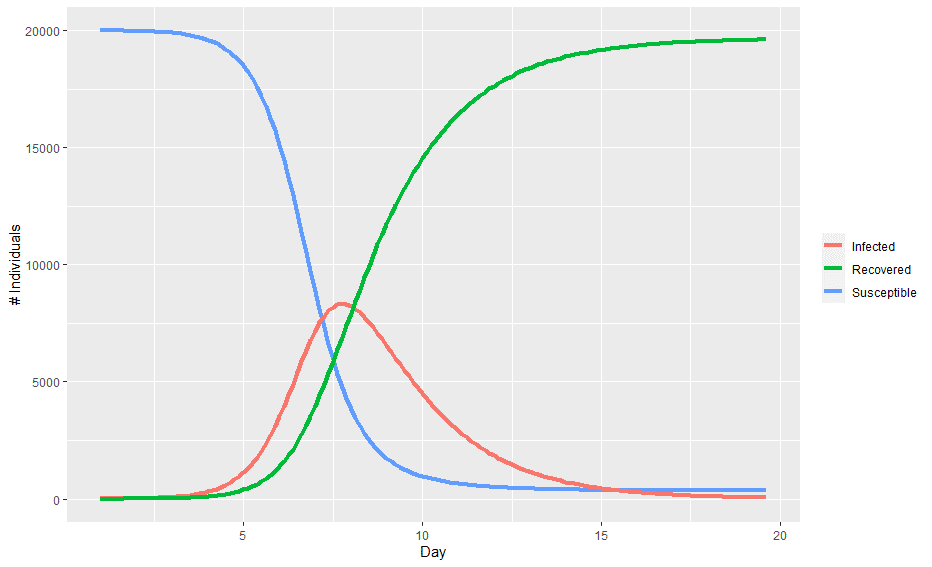
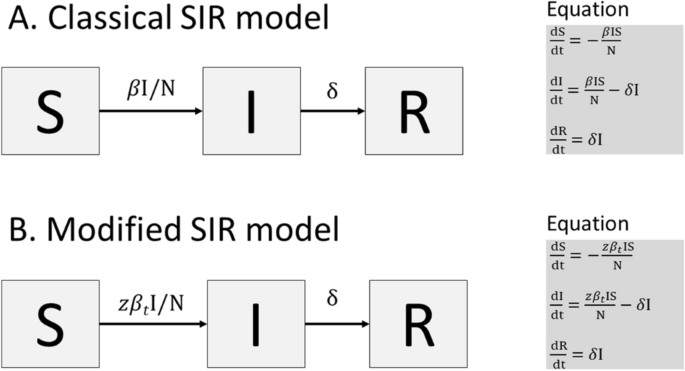
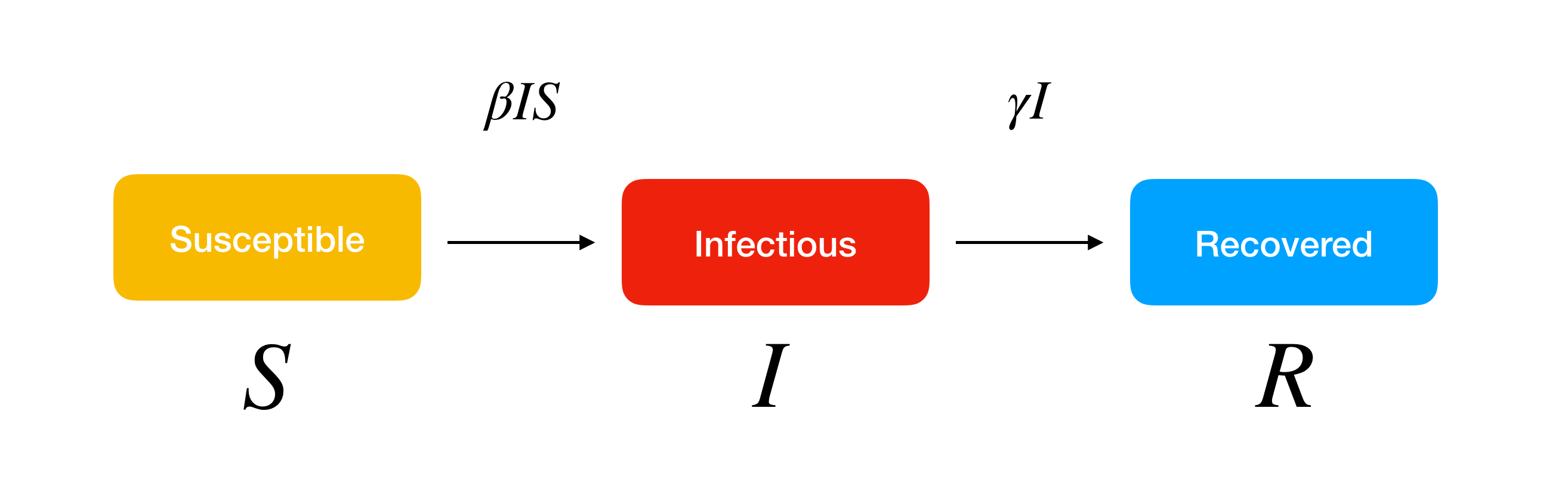
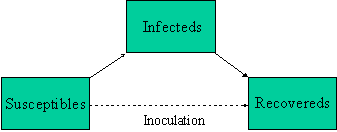
S_t the number of susceptibles in day t I_t the number of infectives in day t R_t. SIR model is of course a very simple model not suitable for shaping complex dynamics especially those which involve large and different populations. It examines how an infected population spreads a disease to a susceptible population which transforms into a recovered population. Of course for the SIR model we want the dependent variable names to be s i and r. Thus inoculation creates a direct path from the susceptible group to the recovered group without passing through the infected group see the diagram below. The SIR Model for Spread of Disease - Background. We consider two related sets of dependent variables. During the winter of 1968-1969 the United States was swept by a virulent new strain of influenza named Hong Kong flu for its place of discovery. The independent variable is time t measured in days.
SIR model for COVID-19 According to this model and without any intervention to contain the spread the virus would be extinguished in about 180 days saving less than 20 of the population. The point of inoculation is to create herd immunity by stimulating in as many people as possible the antibodies that confer immunity -- but without actually giving those people the disease. The use of mathematics to model the spread of infectious disease is an increasingly critical tool not just for epidemiologists and health care providers. The SIR Model for Spread of Disease - Herd Immunity. The SIR model of an infectious disease The model I will introduce is the Susceptible Infected and Recovered SIR model. Compare your calculated value with the one you get by direct calculation from the definition c bk. Discrete SIR infectious disease model part 2.



















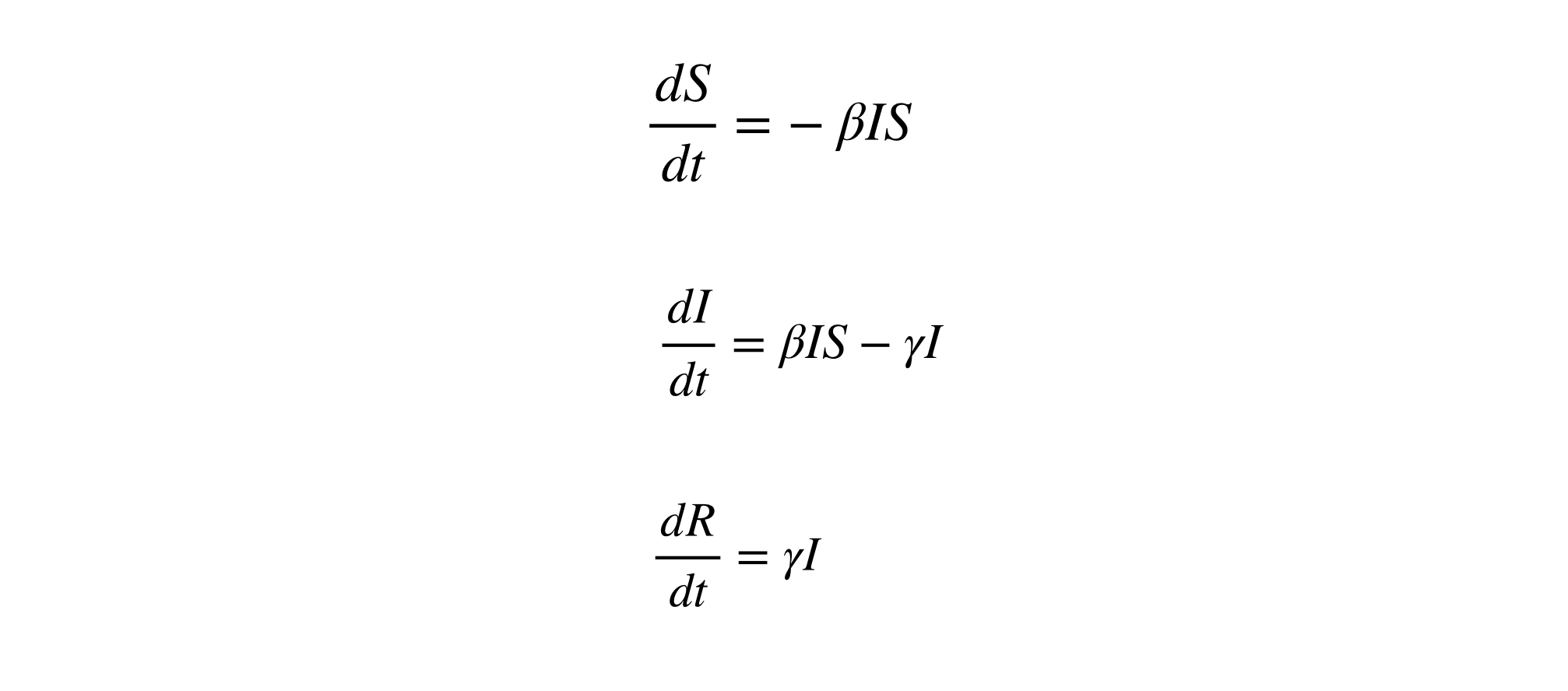










Posting Komentar untuk "The Sir Model For Spread Of Disease"